Főbb különbség: A matematikában egy egyenletet használunk a két kifejezés közötti egyenlőség jelzésére. A függvény viszont sokkal összetettebb, mint egy egyenlet. A függvény a bemenetek halmaza és a megfelelő kimenetek egy csoportja közötti kapcsolat jelzésére szolgál.

Egy egyenlet és egy függvény az algebra két alapja, a matematika tárgya. Mindkettő meglehetősen bonyolult lehet, azonban alapvető formájukban összetéveszthetik egymást. Az egyenlet és a függvény között a fő különbség az, hogy az egyenlet általában egyetlen bemenettel foglalkozik, míg egy függvénynek számos bemenete van.

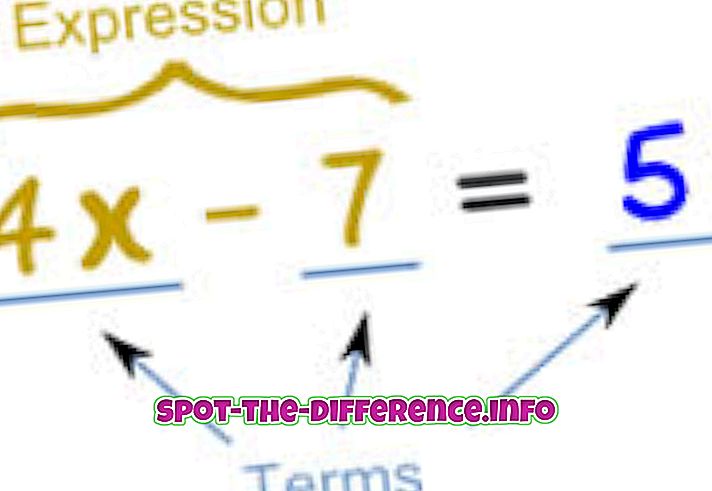
A matematikában egy egyenletet használunk a két kifejezés közötti egyenlőség jelzésére. Lényegében egy egyenletet írnak, mint egy kifejezést, amely megegyezik egy másik kifejezéssel. Például: x + 2 = 5. Ez azt jelenti, hogy bármi legyen x, ha hozzáad 2-et, akkor 5-ös lesz. Ezért megoldhatjuk az x egyenletet, ami 3, 3 + 2 = 5.

Az egyenletek bonyolultabbak lehetnek, és egynél több egyenletet tartalmazhatnak, mint például x, y, z stb. Például: 3x + 2y - z = 4. Minden ábécé azonban egy számnak felel meg. Ebben az esetben x = 1, y = 2 és z = 3.

Ennélfogva,

3x + 2y - z = 4 lesz

3 (1) + 2 (2) - 3 = 4, ami

3 + 4 - 3 = 4 lényegében

4 = 4

A függvény viszont sokkal összetettebb, mint egy egyenlet. A függvény a bemenetek halmaza és a megfelelő kimenetek egy csoportja közötti kapcsolat jelzésére szolgál. Lényegében egy bemenetnek egyetlen kimenetet kell adnia. A függvény két változó közötti kapcsolat. Például: f (x) = x + 2. A funkciónak megfelelően, bármi legyen is, a bemenet egyetlen kimenetet fog adni, ami a bemenet plusz 2. Megoldjuk ezt a funkciót:

Bemenet	Funkció	kibocsátás
x	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Stb…

A függvények különböző alkalmazási területei vannak a matematikában, a fizikában, a számítástechnikában stb. A függvény egy olyan gépnek tekinthető, amely kimenetet ad egy bemenetnek, és ez a kimenet valahogy kapcsolódik a bemenethez.

A funkciónak mindig három része van: a bemenet, a kapcsolat és a kimenet. A függvény klasszikus írási módja az "f (x) = ...", ahol az x a bemenetet, az f (x) pedig a kimenetet jelenti.

Amint a fentiekben említettük, az egyenlet és a függvény között a fő különbség az, hogy az egyenletnek általában csak egy bemenete van, ami az egyenlőséghez vezet. Míg egy funkciónak különböző bemenetei vannak, amelyek mindegyike kimenetet fog adni.