Kulcskülönbség: A pont olyan pont, amely egy végtelen téren vagy sík felületen megjelölt helyet jelöl. A vonal egydimenziósnak tekinthető, és egyenes objektumokat jelentett be, szélesség és mélység nélkül. A sík kétdimenziós sík felület, amely végtelenül nagy, nulla vastagságú.
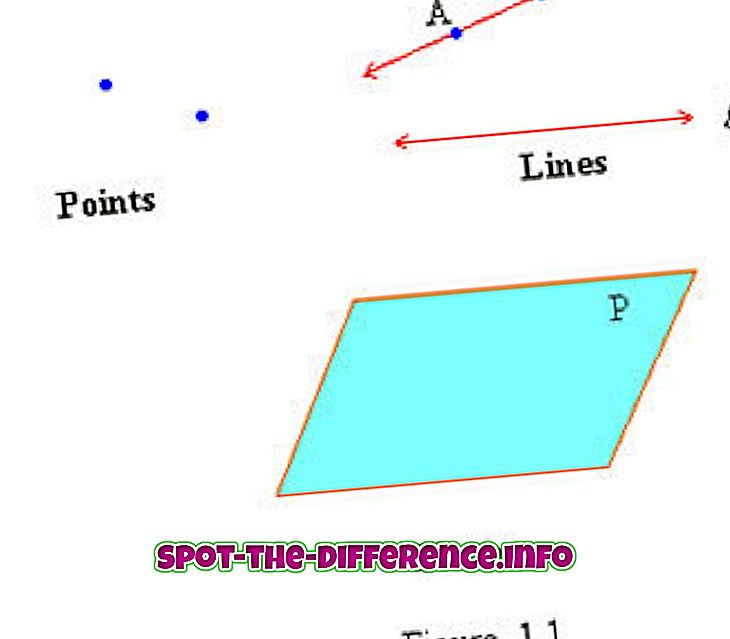
A pont, a vonal és a sík a geometria meghatározatlan fogalmának tekintendő, mert nem formálisan vannak meghatározva. Amikor egy kifejezést definiálunk, általában a szavak leírására egyszerűbb szavakat használ. Azonban egy pontot, vonalat és síkot már egyszerűsítettnek tekintünk. Minden más geometriai fogalom a ponton, a vonalon és a síkon épül. De próbáljuk meg megérteni ezeket a három meghatározatlan kifejezést.
Egy pont olyan pont, amely nem jelez dologot, hanem helyet. A pont olyan helyet jelöl, amely a végtelen térben vagy sík felületen van jelölve. A pont lehet bármilyen méretű pont, de nem rendelkezik hosszúsággal, szélességgel vagy vastagsággal. Ez azért van, mert helyet képvisel, és nem egy dolog.
A pontokat egy nagybetűs betűvel (például A, B, C stb.) Nevezzük. Kétdimenziós euklideszi térben, jobban ismert mint rács vagy egy x-tengelyes és y-tengelyes grafikon, egy pontot egy rendezett pár (x, y). Az x a pont vízszintes elhelyezését jelenti, míg az y a függőleges elhelyezés. Két pontból áll: Collinear és coplanar. A pontok halmaza egyenes vonalban fekszik, míg a síkvonalak egy síkban vannak.
A vonal egydimenziósnak tekinthető, és egyenes objektumokat jelentett be, szélesség és mélység nélkül. A vonal meghatározása a geometria típusától függ. Euklideszi geometriában a vonal nincs meghatározva. Az analitikus geometriában a síkon lévő vonal olyan pontok halmaza, amelyek koordinátái egy adott lineáris egyenletnek felelnek meg. Az előfordulási geometriában egy vonal független objektum lehet a rajta fekvő pontokból.
Egy vonal elfogadott egydimenziós, végtelen számú, összekapcsolt pontként. Egy egyenes egy sík bármely két pontja közötti legrövidebb távolság. A vonalak mindegyik végén két nyíllal vannak jelölve, ami azt jelenti, hogy soha nem ér véget. A sorokat kétféleképpen nevezik: a sor két pontján vagy egy kis kis kurzív betűvel. A vonalon megjelölt két pont használható egy vonalra. Például: A H, I pontok sora HI jelzéssel lesz ellátva, és egy tetejére kerül, amely azt jelenti, hogy egy vonal.
A sík kétdimenziós sík felület, amely végtelenül nagy, nulla vastagságú. A sík kétdimenziós analógja egy pontnak (nulla dimenzió), egy vonal (egydimenziós) és egy szilárd (háromdimenziós). Az euklideszi tér fogalmának meghatározásakor a sík az egész térre vonatkozik. Képzeljünk el egy vastagságú fémlemezt, de örökké örökké folytatódik. Ez síknak tekinthető.
A Wikipedia kimondja: „a matematika, a geometria, a trigonometria, a gráfelmélet és a grafika sok alapvető feladata kétdimenziós térben, vagyis a síkban történik.” Bár a sík végtelen, a rajz érdekében élek. Ezeket a síkokat két párhuzamos pár alkotja, és úgy néz ki, mint egy ferde téglalap. A sík két dimenzióval rendelkezik: hossza és szélessége. De mivel a gép végtelenül nagy, a hossz és a szélesség nem mérhető.
A repülőgépeket három pont határozza meg. Kétféle sík van: párhuzamos síkok és metsző síkok. A párhuzamos síkok két vagy több olyan sík, amelyek végtelenül haladnak egymás útjainál. Képzelje el a korábbi fémlemezt, most adjon hozzá egy másik fémlapot, amely rá van helyezve, és örökre folytatódik. Ez a két párhuzamos sík, amely soha nem keresztezi egymást. Az érdekes repülőgépek azonban pontosan ezt jelentik. Ezek két sík keresztezik egymást. A repülőgépeket általában egy nagybetűvel írják, melyet kurzívan írtak (P sík).
A geometriában a pont, a vonal és a sík egy posztulátum formájában csatlakoznak. Ez a posztulátum három feltételezés (axióma) gyűjteménye, amelyek az euklideszi geometria alapjaként használhatók három vagy több dimenzióban. A három feltételezés magában foglalja: Egyedi vonalfeltételezés, Számlista feltételezés és dimenziós feltételezés. Az egyedülálló vonalfeltétel azt sugallja, hogy pontosan egy sor halad át két különböző ponton. A számsor-feltételezés minden sorban olyan pontok halmaza, amelyek egy-egy-egybe való illesztésre kerülnek a valós számokkal. Bármely pont megfelelhet 0-nak (nulla), és bármely más pont megfelelhet 1-nek (egy). Végül, a dimenziófeltevések egy síkban megadott sort adnak meg, legalább egy pont van a síkban, amely nem a vonalban van. A térben lévő sík miatt legalább egy pont van a térben, ami nem a síkban van.